This page
helps you to understand me better
The
same page as pdf, jpg.
Dozen definitions of the Nijenhuis tensor 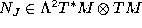 of an almost complex structure
of an almost complex structure 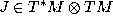 .
.
This tensor is an obstruction for an almost complex structure
to origin from the complex structure.
-
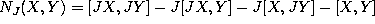 ,
, 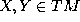 ,
where the right hand side is calculated for arbitrary vector fields
X,Y with the given values
,
where the right hand side is calculated for arbitrary vector fields
X,Y with the given values 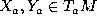 at the point
at the point 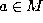 .
In coordinates it has the formula [NN], [NW]:
.
In coordinates it has the formula [NN], [NW]:
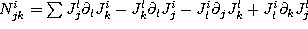 .
. -
J-antilinear by each argument part of the torsion of any almost
complex connection
 (i.e. such a connection that
(i.e. such a connection that 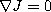 )
)
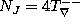 . In other words,
. In other words,
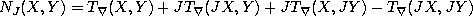 .
There are connections
.
There are connections  called minimal such that
called minimal such that 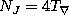 .
[Li].
.
[Li]. - Nijenhuis-Frölicher bracket (differential concomitant)
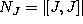 of the vector valued 1-form J with itself. [FN].
of the vector valued 1-form J with itself. [FN]. - Let
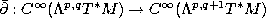 be the component of the de Rham differential. The Nijenhuis tensor is the
only obstruction for the Dolbeault sequence to be a complex [Hö]:
be the component of the de Rham differential. The Nijenhuis tensor is the
only obstruction for the Dolbeault sequence to be a complex [Hö]: 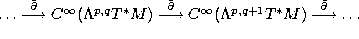
-
Structure function of the first order 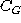 for the G-structure
with
for the G-structure
with 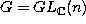 associated with the almost complex structure J.
[St].
associated with the almost complex structure J.
[St].
-
Weyl tensor 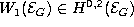 of
the homogeneous PDE (geometrical structure) modeled on the affine complex
space
of
the homogeneous PDE (geometrical structure) modeled on the affine complex
space 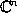 ; the group
; the group 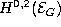 is the second
Spencer cohomology group. [KL].
is the second
Spencer cohomology group. [KL].
-
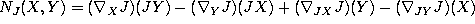 ,
where
,
where 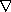 is any symmetric connection on M. [K1].
is any symmetric connection on M. [K1]. - Let g be a compatible metric, i.e.
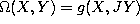 is a
2-form. Then the Nijenhuis tensor can be found from the following formula,
where
is a
2-form. Then the Nijenhuis tensor can be found from the following formula,
where 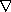 is the Levi-Civita connection of g (hence symmetric, see
7) [KN]:
is the Levi-Civita connection of g (hence symmetric, see
7) [KN]:
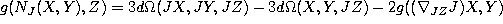 .
. - Let
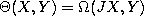 be 2-form (not metric as in 8). Then
we can define the tensor by the formula
be 2-form (not metric as in 8). Then
we can define the tensor by the formula 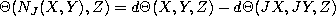 . In the case when
. In the case when 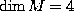 we can divide
we can divide 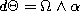 and
and
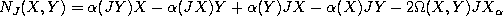 ,
where
,
where 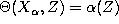 . [K2]
. [K2] - The second generator of the invariant tensor algebra
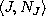 describing the image of the projection
describing the image of the projection
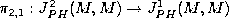 of pseudoholomorphic jets. [K1].
of pseudoholomorphic jets. [K1]. - The real part of the curvature of the distribution
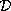 generated by the projector of the complexified space
generated by the projector of the complexified space
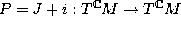 ;
; 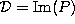 . Hence
. Hence
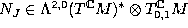 .
[KN], [Ko].
.
[KN], [Ko]. - The homomorphism
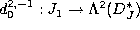 for non-holonomic filtration of the projective module
determined by the module
for non-holonomic filtration of the projective module
determined by the module 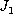 . In the almost complex case
. In the almost complex case 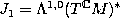 . [LR].
. [LR].
B.K.
References.
- [FN]
- A.Frolicher, A.Nijenhuis ''Theory of vector-valued
differential forms'' (I), Proc. Koninkl. Nederl. Akad. Wetensch., ser.A,
59, issue 3 (1956), 338-359.
- [Hö]
- L.Hörmander, ''The Frobenius-Nirenberg theorem'',
Arkiv for Mathematik 5 (1964), 425-432.
- [KL]
- B.Kruglikov, V.Lychagin ''On equivalence of
differential equations'', Acta et Commentationes Universitatis
Tartuensis de Matematica, 3 (1999), 7-29
- [KN]
- S.Kobayashi, K.Nomizu ''Foundations of Differential Geometry''
II, Wiley-Interscience (1969).
- [Ko]
- J.J.Kohn, ''Harmonic integrals on strongly pseudo-convex
manifolds'' (I), Ann. of Math. 78 (1963), 206-213.
- [K1]
- B.Kruglikov ''Nijenhuis tensors and obstructions for
pseudoholomorphic mapping constructions'', Mathematical Notes 63,
issue 4 (1998), 541-561.
- [K2]
- B.Kruglikov, ''Some classificational problems in four
dimensional geometry: distributions, almost complex structures and
Monge-Ampere equations'', Math. Sbornik, 189, no. 11 (1998), 61-74.
- [Li]
- A.Lichnerowicz ''Theorie globale des connexions et des
groupes d'holonomie'', Roma, Edizioni Cremonese (1955).
- [LR]
- V.Lychagin, V.Rubtsov ''Non-holonomic filtrations:
Algebraic and geometric aspects of non-integrability'', Geometry in Partial
differential equations, Ed. A.Prastaro, Th.M.Rassias (1994), 189-214.
- [NN]
- A.Newlander, L.Nirenberg ''Complex analytic coordinates in
almost-complex manifolds'', Ann. Math. 65, ser. 2, issue 3 (1957),
391-404.
- [NW]
- A.Nijenhuis, W.Wolf ''Some integration problems in
almost-complex and complex manifolds'', Ann. Math. 77 (1963),
424-489.
- [St]
- S. Sternberg ''Lectures on differential geometry'',
Prentice-Hall, New Jersey (1964).
To see the next page click here
Back to the main page |

|
![]() of an almost complex structure
of an almost complex structure ![]() .
.
![]() for the G-structure
with
for the G-structure
with ![]() associated with the almost complex structure J.
[St].
associated with the almost complex structure J.
[St].![]() of
the homogeneous PDE (geometrical structure) modeled on the affine complex
space
of
the homogeneous PDE (geometrical structure) modeled on the affine complex
space ![]() ; the group
; the group ![]() is the second
Spencer cohomology group. [KL].
is the second
Spencer cohomology group. [KL].